Basic Algorithms - 1 - emengjzs Blog

算法，必须把基础的部分重复再重复，不管喜不喜欢。

等价类

两种算法：QuickFind, QuickUnion

基于数组，权衡合并和查找操作时间复杂度，两者不能兼得。

QuickFind

所有等价类均指向同一个元素，合并时需要遍历修改标记。

QuickUnion

每个类对应一个父节点，形成树。
Weighted quick-union ，为了将各个节点到根路径均匀，避免出现长路径，将子节点数作为衡量标准（权重），将权重小的树挂接到权重大的树上。需要另外记录各个节点权重，合并时需要更新权重。
Weighted quick-union by height，将以节点为根节点的树高度作为权重，仅当两个树相同高度时才需要更新权重。
Path compression，为了减小节点到根路径长度，将路径进行压缩。在搜索时将所有访问过的节点全部挂载到根节点，需要遍历两次。

另一种压缩路径是PathHalving，一步两步，将节点挂载到祖父节点，适量权衡更新和查找开销。

int find(int p) {
  while (p != _parent[p]) {
    // notice the two statement order!
    _parent[p] = _parent[_parent[p]];
    p = _parent[p];
  }
  return p;
}

Sorting

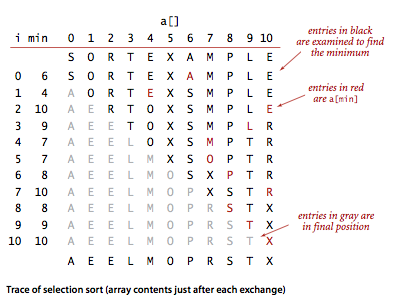
选择排序

关键点：每次在剩余的元素中选取最大/小的元素，然后排在剩余元素的首位

// like <T, Compare<T>> in Java
template<typename T, template <typename> class Compare>
  void selection_sort(std::vector<T>& arr, const Compare<T>& cmp) {
  for (int i = 0; i != arr.size(); ++ i) {
    int max_index = i;
    for (int j = i; j != arr.size(); ++ j) {
      if (cmp(arr[i], arr[j]) < 0) {
        max_index = j;
      }
    }
    if (max_index != i) {
      std::swap(arr[max_index], arr[i]);
    }
  }
}

// usage
vector<int> arr{ 5, 4, 3, 2, 1 };
selection_sort(arr, algs::less<int>());

插入排序

关键点：每次将一个元素插入在之前已排序的列表中的合适位置上。

Move rather than exchange. 对元素进行移动，避免过多的两两交换，相比其他换位算法减少赋值次数。

先拿出（复制）一个待插入元素，这样在数组中的该元素值可以被之后的操作覆盖。
```
T temp = a[i];
```

移动时，只考虑目标操作元素，源目标的值不用考虑清空。

// The item a[i] is moved to a[i + 1]， ignore what is remained in a[i]
a[i + 1] = a[i];  

最后，最后一次移动操作的源目标位置填上刚才复制出的元素

v1:

template<typename T, template<typename> class Compare>
  void insertion_sort(std::vector<T>& arr, const Compare<T>& cmp) {
  for (int i = 0; i < arr.size(); ++ i) {
    T temp = arr[i];
    int j = i - 1;
    while (j >= 0 && cmp(temp, arr[j]) > 0) {
      arr[j + 1] = arr[j];
      -- j;
    }
    arr[j + 1] = temp;
  }
}

sentinel. 设置一个充分条件（哨兵），在退出循环时必定已经完成遍历任务。
sorted detected. 先扫描一遍，若已排序则结束任务，否则，拿取最大/小元素放置在首位，使用冒泡排序，反向遍历

v2:

void insertion_sort(std::vector<T>& arr, const Compare<T>& cmp) {
  // Check if it is sorted.
  bool sorted = true;
  for (int i = arr.size() - 1; i > 0; -- i) {
    if (cmp(arr[i], arr[i - 1]) > 0) {
      std::swap(arr[i], arr[i - 1]);
      sorted = false;
    }
  }
  if (sorted) return;

  // Original insertion sort, notice the i is begin from 1, not 0!
  for (int i = 1; i < arr.size(); ++ i) {
    T temp = arr[i];
    int j = i - 1;
    // Don't have to check if j is out of bound.
    while (cmp(temp, arr[j]) > 0) {
      arr[j + 1] = arr[j];
      -- j;
    }
    // Notice that the index we put temp in is j + 1, not j ! 
    // When a variable breaks from while/for, the value is already invalid
    arr[j + 1] = temp;
  }
}

使用二分查找，找出待插入位置，减少比较次数。

快速排序

Partitioning. 选取一个作为分界点，务必设置为引用。
使用两个指针，i， j在遍历时以low和high为界，不要以j, i为界，因为在循环结束时i，j可能已经不合法。
在扫描时即使遇到和中枢元素相等的元素时也停止循环并进行交换，防止在数组有大量相等元素时退化为线性时间。

template <typename T, template <typename> class Compare>
int _partition(std::vector<T>& arr, const Compare<T>& cmp, int low, int high) {
  T& pivot = arr[low];
  int i = low + 1, j = high;
  while (i < j) {
    // Not 'i < j' because j may be invalid after breaking from loop
    while (i < high && cmp(arr[i], pivot) < 0) ++ i;
    // Not 'j < i' because j may be invalid after breaking from loop
    while (j > low && cmp(arr[j], pivot) > 0) -- j;
    if (i < j) {
      std::swap(arr[i], arr[j]);
    }
  }
  std::swap(arr[low], arr[j]);
  return j;
}

三分中路. 选取一个元素，将小于的元素全部置于左边，大于元素全部置于右边，剩余相等的元素必定在中间。取两个边界less和greater，less之下的小于，greater之上的大于。小的对换时，换来的元素一定小于等于中枢元素，而大的兑换时，换来的元素未进行比较，故遍历的指针不能前进，相对的，遍历到greater边界为止即可。

Basic Algorithms - 1

等价类

QuickFind

QuickUnion

Sorting

选择排序

插入排序

快速排序

FEATURED TAGS

FRIENDS